最近遇到需要在嵌入式开发中使用浮点运算,所以研究了一下float的存储方式,记录一下。
从网上查到float占4个字节,32个bits,涵义如下:

最高位是符号位,其后指数部分8个bits,要减去127才是真实的指数值。小数部分是1.xxxxxxxx…
另外还有NAN的概念,表示未定义或不可表示的结果,例如 0 除以 0 的结果、负数的平方根等。
写了测试程序如下:
#include <stdio.h>
#include <math.h>
#include <stdint.h>
#define prt_flt(x) {\
float fv;\
uint32_t*ip=(uint32_t*)&fv;\
fv = (float)(x);\
printf("%s=%f 0x%08x\n", #x, (float)(x), *ip);\
if(isnan(x))printf("%s is nan\n", #x);\
else printf("%s is not nan\n", #x);\
printf("---------------\n");\
}
void main()
{
printf("float test:\n\n");
prt_flt(0/0.0f);
prt_flt(sqrt(-1));
prt_flt(NAN);
prt_flt(1.5f);
prt_flt(3.1415f);
}
输出如下:
float test:
0/0.0f=-nan 0xffc00000
0/0.0f is nan
---------------
sqrt(-1)=-nan 0xffc00000
sqrt(-1) is nan
---------------
NAN=nan 0x7fc00000
NAN is nan
---------------
1.5f=1.500000 0x3fc00000
1.5f is not nan
---------------
3.1415f=3.141500 0x40490e56
3.1415f is not nan
---------------
我们计算一下0x40490e56是否是3.1415,先展开为2进制表示为
s| exponent| fraction
0100 0000 0100 1001 0000 1110 0101 0110
按上面的规则,这是正数,指数为0x80-127=1;
二进制小数部分为:
1.1001 0010 0001 1100 1010 110
结合指数1,最后的二进制值为
11.0010 0100 0011 1001 0101 10
转成10进制为:
-3 -6 -11 -12 -13 -16 -18 -20 -21
3 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2
= 3+1/8+1/64+1/2048+1/4096+1/8192+1/65536+1/262144+1/524288
= 3+(65536+8192+256+128+64+8+2+1)/524288
= 3+74187/524288
= 3+0.1415004730224609375
= 3.1415004730224609375
我们再看NAN的值0x7fc00000按上述换算是多少:
| |
0111 1111 1100 0000 0000 0000 0000 0000
正数,指数部分0xff-127=128,小数部分二进制1.1,所以为
128
1.5*2
不过,IEEE754标准规定指数部分为全1时表示NAN或infinity,指数全0表示subnormal number,所以指数实际可以取值的范围-126-127;
特殊float的存储特征:
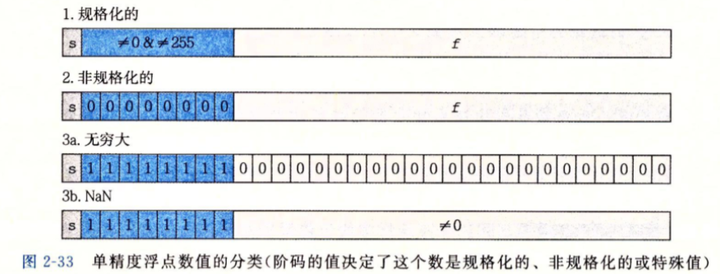
以上参考了知乎:IEEE754标准: 一 , 浮点数在内存中的存储方式及其系列文章,在此表示感谢!